Defining Areas by Curvature Segmentation

This task will show you how to define areas on a mesh along the curvatures or curvature radii.

There are five curvatures:

  • Maximum,
  • Minimum,
  • Mean,
  • Gaussian,
  • Absolute.

The geometric construction of the maximum and minimum curvatures is the following:
let be a plane containing the normal to the surface in a given point.
This plane cuts the surface along a curve that has a given curvature in this point.
If this plane rotates around the normal, the curvatures of the curves intersecting
the surface will vary between two utmost values.
These two values are the maximum (KM) and the minimum (Km) curvatures.

The mean curvature is equal to (KM+Km)/2.
The utmost values appear where the surface is the most warped.
The mean curvature is largely used to detect irregularities on the surface.
A minimal surface is characterized by a null mean curvature.

The gaussian curvature is equal to KM.Km.
It describes the local shape of a surface in one point:

  • if it is positive, the point is elliptic,
    i.e. the surface has locally the shape of an ellipsoid around that point,
  • if it is negative, the surface is hyperbolic in this points,
    i.e. the local shape is a horse saddle,
  • it it is null, the surface is parabolic in this point,
    i.e. one of the maximum or minimum curvatures is null in this point.
    The cone and the cylinder are two surfaces where all points are parabolic.

The absolute curvature is equal to |KM|+|Km|.
It is used to detect the surface areas where the surface is locally almost flat
(the absolute curvature is almost null).

The curvature radii are the inverse of the corresponding curvatures.
Only the maximum and the minimum radii are relevant.
It is carried out on meshes only.
Noisy digitized data are difficult to process.
Open the Curvature01.CATPart from the samples directory.

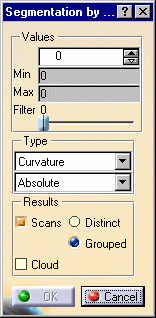
  1. Click Segmentation by Curvature Criterion .
    The dialog box is displayed.

  2. Select the mesh to analyze.

  3. Select the type of analysis from the list: Curvature or Radius.
    Sweep the mesh with the cursor:
    The value of the curvature or the radius is displayed dynamically as you move the cursor:

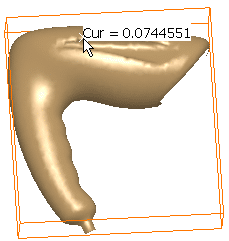
    This is especially helpful to retrieve the value of fillets.

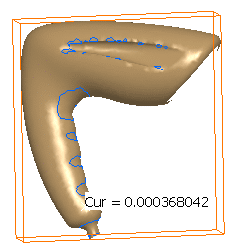
  4. Click mesh: scans are displayed: combine the types of analysis and
    the value in the top spinner box to display scans according to your needs:

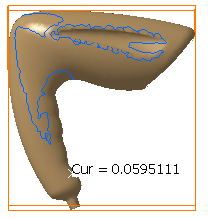
  5. Use the Filter cursor to remove unwanted points.

  6. Click OK to create the result. You can choose to create:

    • Scans, either distinct or grouped:

      Scans.x       elements are created in the specification tree.

    • or Clouds, that is sub-meshs:

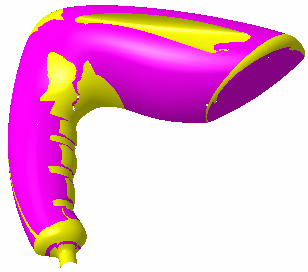
      SubMesh.x elements are created in the specification tree.

      These meshs can then be processed with the Basic Surface Recognition action, for example.

    The input mesh is sent to the NoShow.