This section will help you read the information given in
the Measure Inertia dialog box for Inertia Matrix / G, Inertia Matrix / O,
Inertia Matrix / P and Inertia Matrix / Axis System A.
Moments and Products of 3D Inertia
Iox
Moment of inertia of the object about the ox axis:
Ioy
Moment of inertia of the object about the oy axis:
Ioz
Moment of inertia of the object about the oz axis:
Pxy
Product of inertia of the object about axes ox and oy:
Pxz
Product of inertia of the object about axes ox and oz:
Pyz
Product of inertia of the object about axes oy and oz:
(where M is the mass of the object; units: kg.m2)
Moments and Products of 2D Inertia
Iox
Moment of inertia of the surface about the ox axis:
Ioy
Moment of inertia of the surface about the oy axis:
Pxy
Product of inertia of the surface about axes ox and oy:
(where A is the surface; units: m4)
Matrix of Inertia
3D Inertia:
2D Inertia:
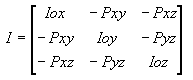
where I is the matrix of inertia of the object with respect to orthonormal basis Oxyz
Moments and
Principal Axes
The matrix of inertia being a real matrix (whose
elements consist entirely of real numbers) and a symmetric matrix, there
exists an orthonormal basis of vectors
in
this matrix of inertia.
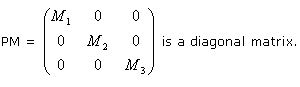
The principal axes are defined by vectors
and
inertia principal moments are expressed by
Note:
is an orthonormal direct basis.
Expression in Any Axis System:
I is the matrix of inertia with respect to orthonormal basis Oxyz.
Huygen's theorem is used to transform the matrix of
inertia:
(parallel axis theorem).
Let I' be the matrix of inertia with respect to orthonormal
basis Pxyz
where 
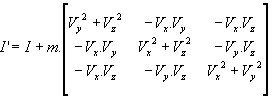
M = {u,v,w}: transformation matrix from basis (Pxyz) to
basis (Puvw)
TM is the transposed matrix of matrix M.
J is the matrix of inertia with respect to an orthonormal basis Puvw:
J = TM.I'.M
Additional Notation Used in Measure
Inertia Command
Ixy = (-Pxy)
Ixz = (-Pxz)
Iyz = (-Pyz)
Note: Since entries for the opposite of the product are symmetrical, they are given only once in the dialog box.
IoxG
Moment of inertia of the object about the ox axis with respect to the system Gxyz, where G is the center of gravity.
IoxO
Moment of inertia of the object about the ox axis with respect to the system Oxyz, where O is the origin of the document.
IoxP
Moment of inertia of the object about the ox axis with respect to the system Pxyz, where P is a selected point.
IoxA
Moment of inertia of the object about the ox axis with respect to the system Axyz, where A is a selected axis system.
etc.