Flex Physical Simulation Overview

This section aims at giving you an overview of the Flex Physical Simulation product.

This overview provides the following information:
 
 

Flex Physical Simulation in a NutshellTop

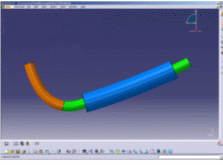
Simulating the behavior of cables (FLEX) using integrated CAD-CAE tools during the product design process is an important requirement in the automotive and aerospace industries. Real components such as flexible tubes, hoses, wires and electrical wires are so flexible that their shape depends totally on the context in which they are used. This behavior has to be correctly taken into account in design and simulation processes.


Flex Physical Simulation is a product dedicated to simulate flexible slender bodies taking into account their physical properties.
 

This product provides other applications, such as Electrical Harness Installation, the functionalities needed to model flexible slender bodies (flex) from the flex definition to its complete flexible behavior in simulation.

Flex Definition Top

 A flex is represented by a:
 

  • 3D curve/line called the neutral fiber
  • variable cross-section
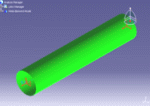
    A typical example of a variable cross-section is as shown: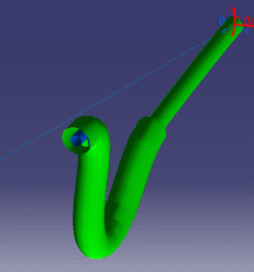

Cross-Sections
 
Only orthotropic cross-sections are supported

An orthotropic cross-section has two symmetry planes meaning the shear section has to fit with the centroid of the section.  
The images below illustrate the various orthotropic cross-section types:

circular cross-section

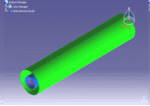annular cross-section
 

rectangular cross-section

arbitrary orthotropic cross-section (elliptic)

Material properties

Flex Physical Simulation product exhibits particular local deformation modes (behavior) of the flex:

  • traction-compression (in axial direction)

  • torsion (around axial direction)

  • bending-shearing (in orthogonal planes containing axial direction)

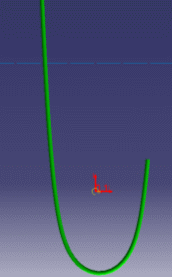
These are examples of more or less flexible flex subjected to gravity with ends imposed  to displacements.

 
 

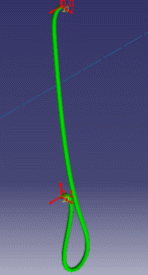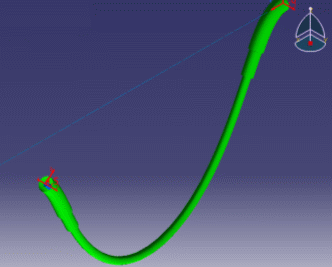 FLEX Added ValuesTop

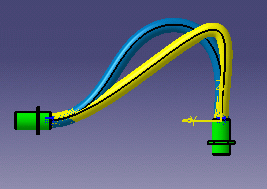
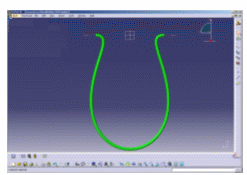
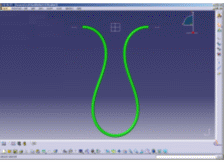
The illustrations below aim at showing you the added value of FLEX in terms of realistic shapes.

Standard algorithm vs FLEX algorithm
Legend:
  • yellow: standard algorithm
  • blue: FLEX algorithm

 

EHI

EHI With FLEX

The covering adds a rigidity that is taken into account by Flex
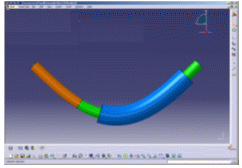Example of the gap that can appear on the curvature.