| Until CATIA V5 R13 | From CATIA V5 R14 | |
| Model Size | [-100 meters, + 100 meters] on each coordinate |
[-1000 meters, + 1000 meters] on each coordinate |
| Model infinite (10 x model size) | [-1000 meters, + 1000 meters] on each coordinate |
[-10000 meters, + 10000 meters] on each coordinate |
Rule 1
Except authorized infinite objects (see rule 2), any relimited objects should be included in the model size. Objects that are not included in the model size are called "infinite".
Rule 2
The authorized infinite objects the user can create are: the planes, lines, half-lines and points. The visualization of such objects is always reframed at most to the model size. The parts of the infinite object that are not in the model size are not seen by the user.
Should an infinite object necessarily fit in the "infinite"?
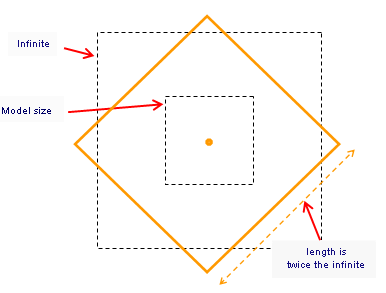
No. An infinite object does not necessarily exactly fit in the model infinite. Usually, its larger coordinates are between half and twice the model infinite.
When a plane is not " parallel " to canonical planes, it is usually not possible to relimit it exactly in the model infinite. When such an infinite plane is created, its half-dimension with the model infinite is determined. Thus a part of it is in the infinite, while a part of it is outside the infinite.
Note: at creation, infinite lines fit in the model infinite.
Transformation of infinite objects are valid provided their origins remain within the model size.

Rule 3
The mathematical definition of an object should be in the model infinite.
An example: the circle arc
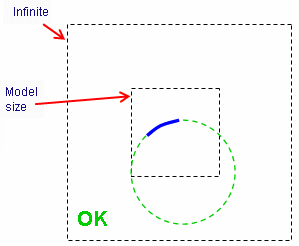
The mathematical definition of the circle consists of a radius which must be smaller than the infinite and a center which must be in the infinite.
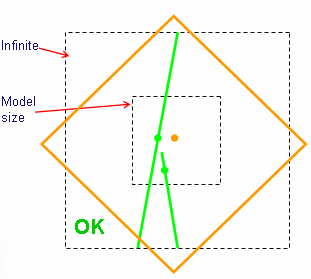
On the left-hand side figure, the created arc circle (in blue) is in the model size, the mathematical circle (in dashed green) is in the infinite (rule 4). This model is valid.
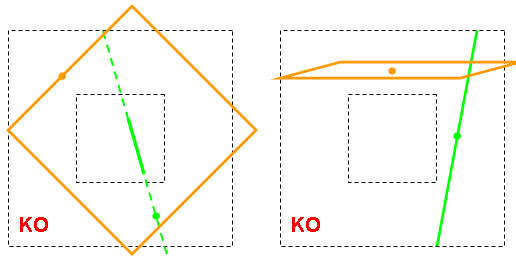
The figures below are examples of unauthorized geometries. On the first figure, the model itself (the full circle in blue) sticks out from the model size:
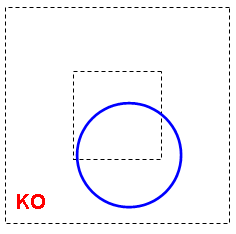
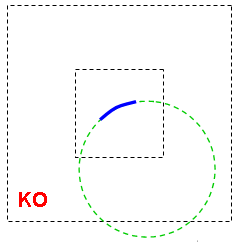
Rule 4
The origin of planes and lines should be in the model size.
An example: the infinite line
On the left-hand side figure, the infinite line and semi infinite line (in green) have their origin (green point) in the model size. The origin (orange point) of infinite plane has its origin in the model size: