About the Computations Results Tab
Algorithms
Description
Simulated
Annealing (global search):
All constraints
are introduced at once in the algorithm. Priorities are handled by assigning
weights corresponding to priorities to each constraint. A global function which
regroups the objective and the modified constraints constitute the new
objective function of the optimization.
Gradient Based
Methods (Local search):
All the
constraints must be differentiable as well as the objective function. The
optimizer takes each constraint modified by its weight into account during the
optimization process. The weights impact the search direction of the gradient.
Thus in both cases modifying the weights might lead to different solutions for
the same problem definition.
Priorities are handled at 2 levels:
- Constraints are handled a priori in the algorithms for
better convergence.
- Priorities are handled in the results post-processing
to identify the best results according to the objective and constraints
priorities. Constraints values are sorted from the highest to the lowest
constraint priority starting from the highest priority.
- For two equivalent values of a given constraint the
order is based on the next priority constraint (lexicographic order).
- When several constraints have equivalent priority a
Pareto order is used to define the classification (i.e. a solution is
equivalent to another solution if improving one constraint of same priority
make (at least) another constraint worst. A solution is better if at least
one constraint of the same priority is improved leaving the others unchanged
or improved.).
Lexicographic order
Priorities are all different
|
Constraints |
C1 |
C2 |
C3 |
Index # |
Class # |
| Priorities |
2 |
3 |
1 |
|
|
| Values |
10 |
20 |
30 |
1 |
5 |
| |
10 |
3 |
2 |
2 |
2* |
| |
3 |
7 |
9 |
3 |
4 |
| |
7 |
3 |
8 |
4 |
1* |
| |
3 |
6 |
8 |
5 |
3 |
|
In the table opposite, to
know which row is the best, we first compare the values of c2 (highest
Priority: 3). If they are equal, we compare the
values of c1 (example of Class # 2* and 1*) and so on in case of equality. |
| Constraints |
C1 |
C2 |
C3 |
Index # |
Class # |
| Priorities |
2 |
1 |
3 |
|
2 |
| Values |
10 |
20 |
30 |
1 |
5 |
| |
10 |
3 |
2 |
2 |
1 (based on c1) |
| |
3 |
7 |
9 |
3 |
4 |
| |
7 |
3 |
8 |
4 |
3* (based on c1
because c3 values are equal) |
| |
6 |
3 |
8 |
5 |
2* |
|
In the table opposite,
the C1 values must be taken into account because C2 and C1 values are
equal. |
 |
- When priorities are
all equal, the only equivalence of 2 solutions occurs when all
constraint values are equal between the 2 different solutions.
- Changing priorities changes the ranking of the
solutions (Class #)
|
Some Priorities are equal
| Constraints |
C1 |
C2 |
C3 |
Index # |
Class # |
| Priorities |
1 |
2 |
2 |
|
|
| Values |
10 |
20 |
30 |
1 |
4 |
| |
7 |
2 |
3 |
2 |
1* |
| |
3 |
7 |
9 |
3 |
3 |
| |
7 |
3 |
2 |
4 |
1* |
| |
3 |
6 |
9 |
5 |
2 |
|
In the table opposite, if
you consider only C1 and C2 values, 3 solutions are identical: 5, 4
and 2. Solution 3 is the intermediate solution and 1 is the worst
If you consider, all constraints, you get the following order, going from
the best to the worst: 2, 4, 5, 3, 1. |
* Both solutions are equivalent: When c2 increases, c3
decreases and conversely. Furthermore c1 is equal in both cases.
All Priorities are equal
| Constraints |
C1 |
C2 |
C3 |
Index # |
Class # |
| Priorities |
1 |
1 |
1 |
|
|
| Values |
10 |
20 |
30 |
1 |
2* |
| |
10 |
3 |
2 |
2 |
1 |
| |
3 |
7 |
8 |
3 |
1 |
| |
7 |
3 |
8 |
4 |
1 |
| |
3 |
6 |
9 |
|
1 |
|
In the table opposite, all
solutions are strictly equivalent except 2. *
All values are worse. |
Analyzing Results
 |
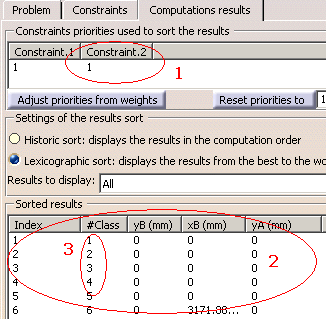- The results of the optimization are displayed in
the Computations Results tab of the Optimization dialog box
(2).
- Note that priorities are displayed in this tab
and can be changed (1). Modifying a
constraint priority in this tab will only impact the Lexicographic sort
and not the algorithm.
- Several constraints can have the same
priorities, results can be multiple (i.e. equivalent solutions). Those
solutions are presented in decreasing order of significance.
- The #Class column is the quality of
the solution(3). Solutions
belonging to the same class are equivalent.
- Adjust priorities from weights: Allows to sort the constraints in
the order dictated by the weights assigned for each constraint in the
Constraints tab page.
|
Filtering Results
The results list can be filtered to restrict the number
of solutions displayed and to re-order solutions:
- Historic sort: The results are displayed in
the order of exploration by the algorithm.
- Lexicographic sort: The solutions are
sorted in lexicographic order (the highest priority first). In case of
equivalence (i.e. constraints with same weights), they appear in historic
order but with the same class.
Filters can also be applied to constraints values. A
combo list enables you to select the desired filter:
 |
All: All
solutions will be displayed. All
constraints satisfied only: Only solutions with satisfied
constraints will be displayed.
User defined: Only the items you
selected will be displayed in the sorted list. |
Selecting a Solution
It is possible to select a solution by clicking the
and to apply it to the
parameters.