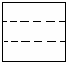
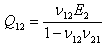Vibration of Simply Supported Laminated Plates

The purpose of this test is to check laminated plates with orthotropic materials.
You will use 2D meshes.

Reference:

Mechanics of Composite Materials, Robert M. Jones, Hemisphere Publishing Corporation, chap 5.5.1, p270.
 

Specifications

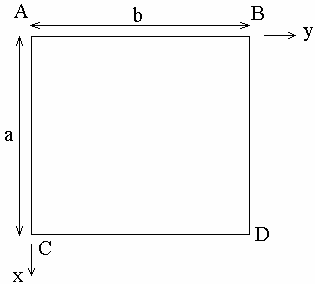
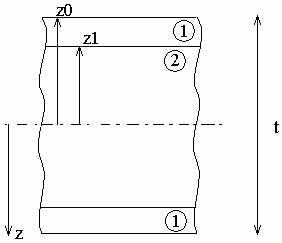
Geometry Specifications

a = 0.1 m
b = 0.1 m
t1 = t3 = 0.0001 m
t2 = 0.0004 m

 

Analysis Specifications

  • Material 1:

    • Young Modulus (material):

      E1 = 2 x 1011 Pa
      E2 = 2 x 1010 Pa

    • Poisson's Ratio:
      ν12 = 0.3

    •  Shearing coefficient
      G12 = G23 = G13 = 5.169 x 109 Pa

    • Density:
      = 6000 kg x m-3

  • Material 2:

    • Young Modulus (material):

      E1 = 7 x 1010 Pa
      E2 = 7 x 109 Pa

    • Poisson's Ratio:
      ν12 = 0.2

    •  Shearing coefficient
      G12 = G23 = G13 = 3.203 x 109 Pa

    • Density:
      = 6000 kg x m-3

Mesh Specifications:

  • 2D mesh with linear quadrangle elements (QD4)

  • Mesh size: 2 mm

Restraints (User-defined):
On AB, CD, AC and BD: translation along Z = 0
 

Results

Analytical Results

 

For a simply supported plate, we have:

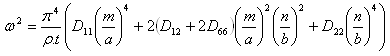
where:

 

Conditions for a specially orthotropic material are:

  • D11 / D22 = 10

  • D12 + 2D66 = 1

 

m: transversal vibration mode
n: longitudinal vibration mode

Computed Results

Modes

Reference results [Hz]

Computed results [Hz]

Normalized results

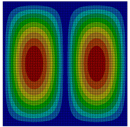
Visualization

m = 1
n = 1

242.724

242.16

0.997676

m = 1
n = 2

390.785

389.992

0.997971

m = 1
n = 3

702.403

701.991

0.999413

m = 2
n = 1

880.240

874.553

0.99354

To Perform the Test:

The orthotropic_laminates.CATAnalysis document presents a complete analysis of this case.

To compute the case, proceed as follow:

  1. Open the CATAnalysis document.

  2. Compute the case in the Generative Structural Analysis workbench.