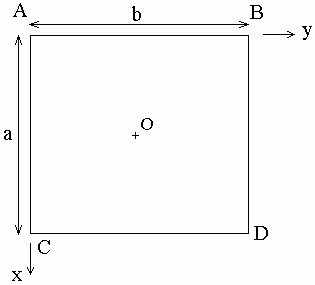
Laminated Plates with Orientation

The purpose of this test is to check laminated plates with orthotropic materials using an angle of orientation.
You will use 2D meshes.

Reference:

3D model with parabolic hexahedron elements (HE20), computed with CATIA.
 

Specifications

Geometry Specifications

Angle:
plate 1 = 90 deg
plate 2 = 30 deg

a = 0.1 m
b = 0.1 m
t1 = 0.0002 m
t2 = 0.0004 m

 

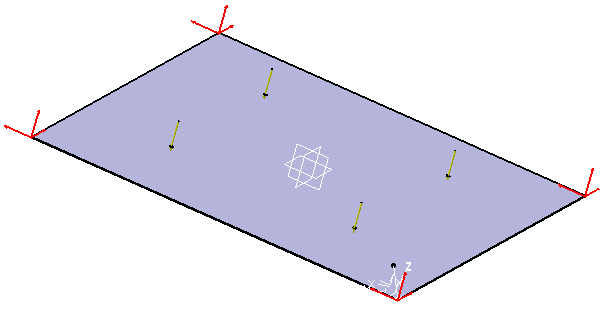
Analysis Specifications

  • Material 1:

    • Young Modulus (material):

      E1 = 341.6 x 106 Pa
      E2 = 179.3 x 106 Pa

    • Poisson's Ratio:
      ν12 = 0.44

    •  Shearing coefficient
      G12 = 100 x 106 Pa
      G23 = 60.8 x 106 Pa
      G13 = 101.5 x 106 Pa

  • Material 2:

    • Young Modulus (material):

      E1 = 34.16 x 106 Pa
      E2 = 17.93 x 106 Pa

    • Poisson's Ratio:
      ν12 = 0.44

    •  Shearing coefficient
      G12 = 10 x 106 Pa
      G23 = 6.08 x 106 Pa
      G13 = 10.15 x 106 Pa

Mesh Specifications:

  • In both cases, mesh size: 2 mm

    • 2D mesh with linear quadrangle elements (QD4)

    • 3D mesh with parabolic hexahedron elements (HE20)

Restraints (User defined):

  • On AB and CD: translation along Y and Z

  • On AC and BD: translation along X and Z

Loads:
Surface force density: FZ = -10 N/m2

Results

The following results correspond to:

  • The displacement of O along Z (w)
  • The restraint on O in the center of plate 2 (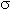xx)

 

3D model (Reference)

 2D model

Normalized results

w [mm]

-3.47697

-3.47213

0.9986

xx [mm]

30358.523

30217.189

0.9953

To Perform the Test:

The laminated_plates.CATAnalysis document presents a complete analysis of this case.

To compute the case, proceed as follow:

  1. Open the CATAnalysis document.

  2. Compute the case in the Generative Structural Analysis workbench.

  3. Create local sensors (Stress tensor and Displacement vector).