Harmonic Forced Vibration of a Plane Grid

This test lets you check analysis results for a plane grid, in the context of an harmonic dynamic response case. You will use a 1D mesh.

This test is used to validate the following attributes:

  • 1D beam elements

  • Harmonic dynamic response solve algorithms.

Reference:

AFNOR technique, SFM Paris, Guide de validation des progiciels de calcul de structures, SSLL 04/89, pp.198-199, 1990.
 

Specifications

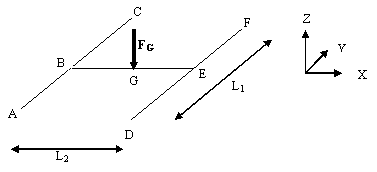
Geometry Specifications

Length:
L1 = L2 = 5 m

Section IPE 200 :

  • area = 2.872e-3 m2

  • Iy = 1.943e-5 m4

  • Iz = 1.424e-6 m4

The geometry is built with two Parts, inserted in a Product. The first Part includes the beam AC and the beam DF. The second Part includes the beam BE.

Analysis Specifications

Young Modulus (material)
E = 200 GPa

Poisson's Ratio (material)
ν = 0.3

Density:
 ρ = 7800 kg/m3

Mesh Specifications:

  • 500 mm elements for the three edges

  • No automatic mesh capture for all

  • For ball joints B and E, rigid connection property with transmitted degrees of freedom
    Tx = Ty = Tz = 0

Restraints (User-defined):

  • At points A, C, D and F : Tx = Ty = Tz = 0

  • Edges AC and DF : Ry = 0

  • Edge BE : Rx = 0

Loads:

  • F = F0 sin ωt

  • Distributed force F0 = -100 000 N

  • ω = 80 rad/s, so f = 12.7324 Hz
 

Results

Frequency Response

Fundamental mode

Frequency [Hz]

Error [%]

Analytical solution

Computed results

1

16.456

16.410

0.28

2

38.165

37.941

0.59

Harmonic Dynamic Response

Displacement on z axis at f = 12.7324 Hz

Point

Type of values

Analytical solution

Computed results

Error [%]

B and E

WBmax [mm]

-98.00

-100.35

2.4

G

WG+WGmax [mm]

-227.00

-226.50

0.2

To Perform the Test:

The Harmonic_forced_vibrations_plane_grid.CATAnalysis document presents a complete analysis of this case.

Proceed as follow:

  1. Open the CATAnalysis document.

  2. Compute the case and generate an image called Deformed mesh.